Focal Loss的理解以及在多分类任务上的使用(Pytorch)

最近在做遥感影像分割，涉及到多个类别，建筑、道路、水体、植被、耕地等等。发现各类别之间占比特别不均衡，会影响最终精度，尝试过使用加权交叉熵，权重计算参考《中值频率平衡:图像分割中计算类别权重的方法》，精度有所提升，但是还是不能满足要求，后来就想试试Focal Loss，发现效果提升明显，这里也从头梳理一下Focal Loss。 个人觉的要真正理解Focal Loss，有三个关键点需要清楚，分别对应基础公式，超参数α，超参数γ。     一、二分类(sigmoid)和多分类(softmax)的交叉熵损失表达形式是有区别的。     二、理解什么是难分类样本，什么是易分类样本？搞清难易分类样本是搞清楚Focal Loss中的超参数γ作用的关键。     三、负样本的α值到底该是0.25还是0.75呢？这个问题对应Focal Loss中的超参数α的调参。 理解上面三点应该就能搞清楚二分类Focal Loss的基本思想，然后就可以推广到多分类问题上。

二分类和多分类的交叉熵的区别具体可以参考文章《一文搞懂交叉熵损失》

在做二分类的任务时，一般是用sigmoid作为最后的激活函数，输出只有一个代表样本为正的概率值p，二分类非正即负，所以样本为负的概率值为1-p。 则以sigmoid作为激活函数的二分类任务交叉熵损失的计算公式为: C E L = − y ∗ l o g ( p ) − ( 1 − y ) ∗ l o g ( 1 − p ) CEL=-y*log(p) -(1-y)*log(1-p) CEL=−y∗log(p)−(1−y)∗log(1−p)   其中 y y y是实际标签，正样本为1，负样本为0，p是sigmoid激活函数的输出值。

在做多分类的时候，一般是以softmax作为最后的激活函数的，输出有多个值，对应每个分类的概率值，和为1。 则以sofmax作为激活函数的多分类任务的交叉熵损失计算公式为 C E L = − ∑ 0 C − 1 y i ∗ l o g ( p i ) = − l o g ( p c ) CEL=-\sum_{0}^{C-1}y_{i}*log(p_{i})=-log(p_{c}) CEL=−0∑C−1​yi​∗log(pi​)=−log(pc​)   其中 p c p_{c} pc​表示softmax激活函数输出结果中第c类的对应的值。 注意:论文中是基于以sigmoid为激活函数来作为二分类交叉熵损失的。我在最开始学Focal Loss的时候老是将sigmoid和softmax混着看，一会用sigmoid来套公式，一会用softmax来套公式，很容易把自己搞蒙。 文章的备注里也指出可以很容易将Focal Loss应用于多分类，为了简单起见，文章中关注的是二分类情况。

论文将交叉熵损失公式做了进一步的简化:

C E ( p , y ) = { − l o g ( p ) i f y = 1 − l o g ( 1 − p ) o t h e r w i s e CE(p,y)=\left\{\begin{matrix} & -log(p)& if\quad y=1\\ & -log(1-p)& otherwise \end{matrix}\right. CE(p,y)={​−log(p)−log(1−p)​ify=1otherwise​ 其中 p t = { p i f y = 1 1 − p o t h e r w i s e p_{t}=\left\{\begin{matrix} &p& if\quad y=1\\ &1-p& otherwise \end{matrix}\right. pt​={​p1−p​ify=1otherwise​ 所以： C E ( p , y ) = C E ( p t ) = − l o g ( p t ) CE(p,y)=CE(p_{t})=-log(p_{t}) CE(p,y)=CE(pt​)=−log(pt​) 这里 p t p_{t} pt​的理解比较关键。 p t p_{t} pt​的大小实际能反映出样本难易分类的程度。 举个例子，当样本为正样本(y=1)时，如果模型预测的p=0.3,表示模型预测该样本为负样本，模型预测错误， p t p_{t} pt​=0.3，如果模型预测的p=0.8，表示模型预测该样本为正样本，模型预测正确， p t p_{t} pt​=0.8。当样本为负样本(y=0)时,如果模型预测的p=0.3，表示模型判断该样本为负样本，判断正确， p t p_{t} pt​=1-p=0.7。如果模型输出的p=0.8，表示模型判断该样本为正样本，模型预测错误， p t p_{t} pt​=1-p=0.2。对应下表: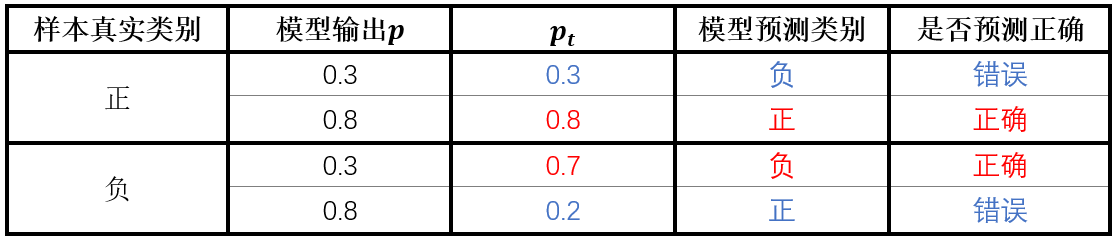

可以看到，不管是正样本还是负样本，模型预测正确时 p t p_{t} pt​都很大，预测错误时 p t p_{t} pt​ 值很小，所以 p t p_{t} pt​值代表了模型对样本预测正确的概率。 接下来看论文中一上来就给的一张图。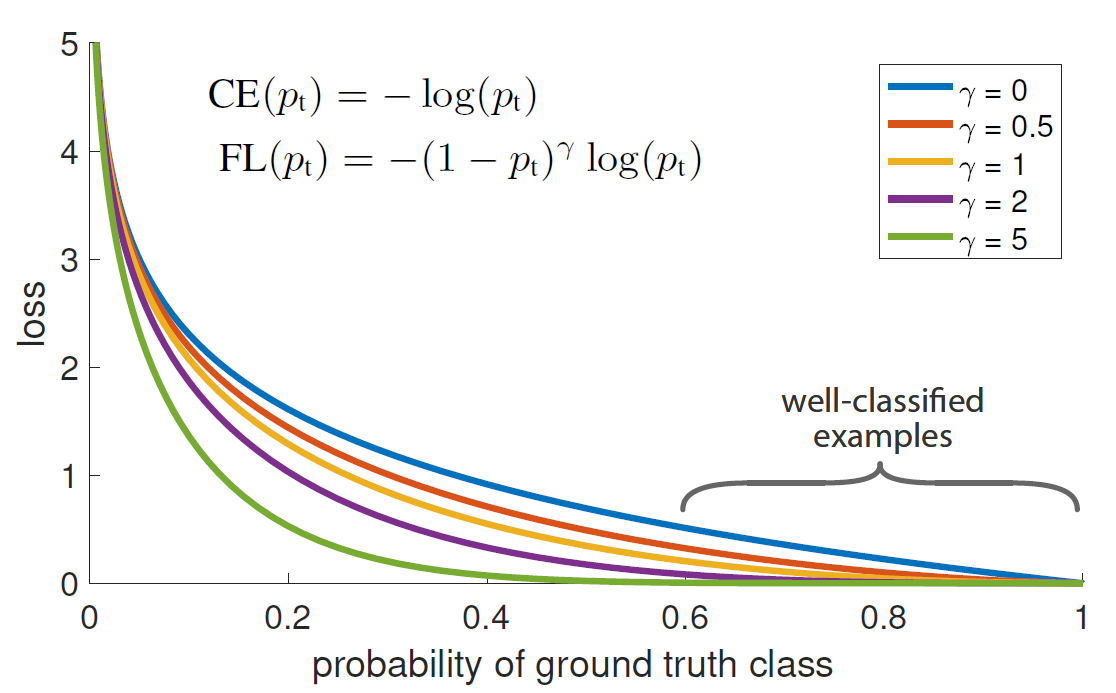

横坐标是 p t p_{t} pt​，可以看出作者指出 p t p_{t} pt​ ∈ \in ∈(0.6,1)区间的样本为well-classified examples（易分类样本）。 针对上面的例子再啰嗦几句，对于一个正样本，如果模型得到的预测的p总是在0.5以上，则说明该样本很容易被分类正确，所以是易分类样本，此时pt=p，pt也总是在0.5以上，如果模型得到的预测的p总是在0.5以下，则说明该样本很难被正确分类，所以为难分类样本，此时pt也总是在0.5以下；同理对于一个负样本，模型预测的p很容易在0.5以下，表明模型很容易将样本正确分类，所以是易分类样本，pt=1-p，pt总是在0.5以上，如果模型得到的预测的p总是在0.5以上，则说明针对这类样本模型总是分类错误，所以是难分类样本，pt=1-p，pt总是在0.5以下。 总结一下,易分类样本的特征: p t p_{t} pt​>0.5；难分类样本特征: p t p_{t} pt​